Published

2025-03-31

Week 1

Basics of python

Create a list!

[1, "a", 3, 60]

[1, 'a', 3, 60]

Save this as an object!

myList = [1, "a", 3, 60]
print(myList)
myList

[1, 'a', 3, 60]

[1, 'a', 3, 60]

myList + [2, 4, 5]

[1, 'a', 3, 60, 2, 4, 5]

myList * 4

[1, 'a', 3, 60, 1, 'a', 3, 60, 1, 'a', 3, 60, 1, 'a', 3, 60]

Markdown

We’ll add some HTML widgets and play around with that.

#reading in modules
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as widgets

Let’s generate 100 random data values using numpy.

rng = np.random.default_rng(12)
vals = rng.standard_normal(100)
vals

array([-6.82677987e-03,  1.04614329e+00,  7.41588421e-01,  7.23956542e-01,
        1.61877622e+00, -1.20555814e+00, -6.26955471e-01, -1.32066321e+00,
       -1.07752508e-01,  9.98763655e-01, -2.19478863e-02,  4.95880066e-01,
       -1.91076866e+00,  1.47064166e-01, -9.06943251e-01,  1.77538939e+00,
        8.86849076e-01,  9.49349483e-01, -5.78549625e-02,  6.12862274e-01,
        6.57890162e-01, -3.44402666e-01, -4.97372035e-01, -1.14772783e-01,
       -6.05452009e-01, -5.94339418e-01, -2.83375376e-01, -7.28417727e-01,
        7.66327786e-01, -1.59608633e+00,  8.23562129e-01, -6.25566470e-01,
       -5.45939956e-01, -1.35084714e+00, -1.44242119e-01, -2.47661509e-01,
        1.91455831e-01, -5.33774296e-01,  9.37561793e-02,  1.81969184e+00,
        4.08999694e-01, -5.73690037e-01,  9.53109595e-01, -1.28801134e-01,
        5.93874468e-01,  6.12747429e-01, -3.91065717e-01, -1.93028750e+00,
       -3.47653623e-01,  5.51455424e-01, -3.80110407e-01,  4.38969315e-01,
        9.79540372e-01, -5.44113415e-01,  1.23135175e+00,  1.62180446e+00,
        1.07904594e+00,  1.16546284e+00,  1.09679645e+00,  2.25453906e+00,
        1.85860905e-01,  2.08408285e-03,  6.03107305e-01, -9.08195119e-01,
       -1.55317676e+00, -8.82007973e-01,  3.72565350e-01,  4.73053341e-01,
       -1.53635872e+00, -1.88346371e+00, -3.16142243e-01, -1.88056516e-01,
       -4.92008330e-02,  6.71362447e-01,  1.22883418e+00,  2.30896430e-01,
        6.12684704e-01, -1.09520169e+00, -1.17630801e+00,  2.36238334e-01,
        6.64663103e-01,  7.26243456e-01,  5.92741991e-01,  7.84173709e-01,
        8.09828030e-01, -1.75218536e+00, -7.34165769e-01,  4.55159742e-01,
        5.96671965e-01, -1.51209241e+00,  1.17306137e+00, -4.38831924e-01,
       -2.32424749e-01,  2.73818645e-01,  7.49635232e-01, -1.43311699e+00,
        9.89912577e-01,  7.72934677e-02, -7.70813495e-01, -2.75273142e-01])

plt.hist(vals)

(array([ 8.,  6.,  6., 17., 15., 12., 24.,  7.,  4.,  1.]),
 array([-1.9302875 , -1.51180484, -1.09332219, -0.67483953, -0.25635687,
         0.16212578,  0.58060844,  0.99909109,  1.41757375,  1.8360564 ,
         2.25453906]),
 <BarContainer object of 10 artists>)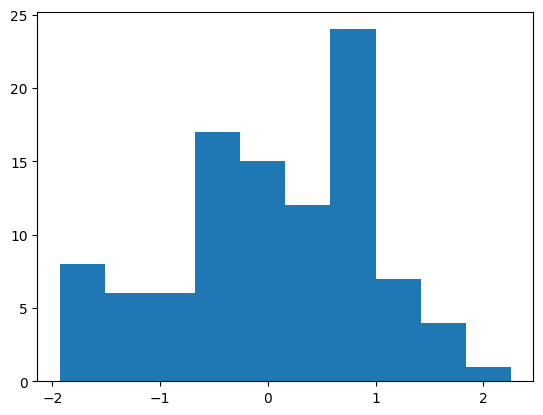

plt.hist(vals, bins = 12)

(array([ 5.,  6.,  5., 11., 13., 12., 11., 19., 11.,  2.,  4.,  1.]),
 array([-1.9302875 , -1.58155195, -1.2328164 , -0.88408086, -0.53534531,
        -0.18660976,  0.16212578,  0.51086133,  0.85959687,  1.20833242,
         1.55706797,  1.90580351,  2.25453906]),
 <BarContainer object of 12 artists>)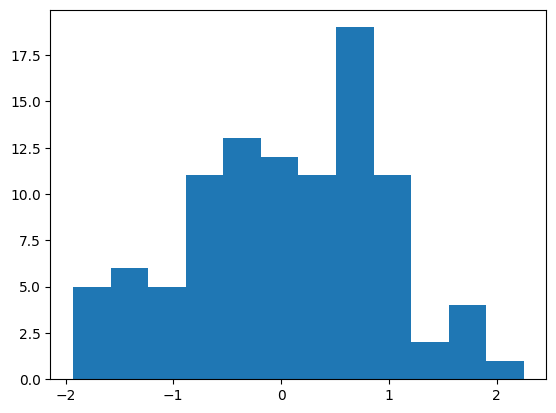

def myPlot(bins):
    plt.hist(vals, bins)

myPlot(4)

widgets.interactive(myPlot, bins =(1,20))

Strings Practice

Here we’ll look at some quick string methods and functions including string formatting!

String formatting

One way to do formatting is to use {} within a string and then use the .format() method. Let’s create a string that we can place values into. Something like this:

“The probability of being less than or equal to 2 for a normal distribution with mean 4 and standard deviation 1 is …”

prob_string = "The probability of being less than or equal to {0} for a normal distribution with mean {1} and standard deviation {2} is {3}"

mean = 1
std = 2
y = 1.55

'The probability of being less than or equal to 1.55 for a normal distribution with mean 1 and standard deviation 2 is 0.6083'

Now pull the scipy.stats stuff from above and insert the numbers using the .format() method.

import scipy.stats as stats
stats.norm.cdf(y, mean, std)

0.6083418808463948

prob_string.format(y, mean, std, round(stats.norm.cdf(y, mean, std), 4))

'The probability of being less than or equal to 1.55 for a normal distribution with mean 1 and standard deviation 2 is 0.6083'

Let’s look at splitting up a big string of text into ‘words’. This is often a first step done when doing a basic sentiment analysis of some text.

First we need a string of text to break up. Project Gutenberg has some classic open works that you can get the entire text from. Here we’ll pull from a cookbook called Practical Vegetarian Cookery. We’ll just grab two recipes:

WINTER VEGETABLE PIE.

Place in baking dish, slices of cold boiled potatoes, onions, celery, and carrot, then add one scant cupful of stewed tomatoes and one half can of peas. Cover with stock, thickened to a gravy with butter and flour, cover with plain crust, and bake. A pie of this nature can be made with a great variety of ingredients; apples, boiled chestnuts, onions, and potatoes make a good combination. Rice, with a grating of cheese, celery, onion, and tomato, another variety.

VEGETABLE HASH.

Of cooked and chopped vegetables, use one carrot, one blood beet, two turnips, two quarts of finely sliced potatoes, one onion, and a stalk of celery; one sprig of parsley; put them in a stew pan, cover tight, and set in the oven. When thoroughly heated pour over a gravy of drawn butter and cream. Stir together and serve.

Let’s create a string with these and count variables that occur.

recipe = """
WINTER VEGETABLE PIE.

Place in baking dish, slices of cold boiled potatoes, onions, celery,
and carrot, then add one scant cupful of stewed tomatoes and one half
can of peas. Cover with stock, thickened to a gravy with butter and
flour, cover with plain crust, and bake. A pie of this nature can be
made with a great variety of ingredients; apples, boiled chestnuts,
onions, and potatoes make a good combination. Rice, with a grating of
cheese, celery, onion, and tomato, another variety.

VEGETABLE HASH.

Of cooked and chopped vegetables, use one carrot, one blood beet, two
turnips, two quarts of finely sliced potatoes, one onion, and a stalk
of celery; one sprig of parsley; put them in a stew pan, cover tight,
and set in the oven. When thoroughly heated pour over a gravy of drawn
butter and cream. Stir together and serve.
"""
recipe

'\nWINTER VEGETABLE PIE.\n\nPlace in baking dish, slices of cold boiled potatoes, onions, celery,\nand carrot, then add one scant cupful of stewed tomatoes and one half\ncan of peas. Cover with stock, thickened to a gravy with butter and\nflour, cover with plain crust, and bake. A pie of this nature can be\nmade with a great variety of ingredients; apples, boiled chestnuts,\nonions, and potatoes make a good combination. Rice, with a grating of\ncheese, celery, onion, and tomato, another variety.\n\nVEGETABLE HASH.\n\nOf cooked and chopped vegetables, use one carrot, one blood beet, two\nturnips, two quarts of finely sliced potatoes, one onion, and a stalk\nof celery; one sprig of parsley; put them in a stew pan, cover tight,\nand set in the oven. When thoroughly heated pour over a gravy of drawn\nbutter and cream. Stir together and serve.\n'

Replace the \n, ,, and . values with a space instead. Lowercase everything with the .lower() method and then .strip() to remove the excess whitespace. Finally, the .split() method gives us a list with each element being a word from the document.

recipe_split = recipe.replace("\n", " ") \
  .replace(".", " ") \
  .replace(",", " ") \
  .replace(";", " ") \
  .lower() \
  .strip() \
  .split(" ")

Now we can see how often different words come up.

type(recipe_split)
recipe_split.count("potatoes")

Math Types (Including Booleans)

Remember that things can’t be stored precisely so you may sometimes run into issues where two things should be equal but don’t resolve as equal.

from math import sqrt
sqrt(2)**2 == 2

False

Use the isclose() from numpy to check things like this.

import numpy as np
np.isclose(sqrt(2)**2, 2)

True

We should have an idea about inf, -inf, and nan values in python. nan values can be returned when a mathematical function is used outside of its domain for instance. Here is the norm.ppf() function. This returns the value from the standard normal with a certain proportion of the distribution to the left of it (proportion specified by the value you feed the function). These values should of course be between 0 and 1.

import scipy.stats as stats
stats.norm.ppf(0.5)

0.0

nan

What happens if we give a value like -1?

stats.norm.ppf(-0.1)
np.isnan(stats.norm.ppf(-0.1))

True

Infinite values can pop up too. There are lots of ways to create an infinite value via casting as well.

float(1)
float("Inf")
-float("Inf")

-inf

Let’s update our string from before with digits! (Note that using floating point for z and integers for mean and standard deviation doesn’t really make sense, I’m just showing the functionality!)

prob_string = "The probability of being less than or equal to {y:.2f} for a normal distribution with mean {mean:d} and standard deviation {std:d} is {prob:.4f}"

prob_string.format(y = y, mean = mean, std = std, prob = stats.norm.cdf(y, mean, std))

'The probability of being less than or equal to 1.55 for a normal distribution with mean 1 and standard deviation 2 is 0.6083'

Week 2

User Defined Functions

Let’s create our own plotting function that will plot a Binomial random variables probabilities with a Normal approximation overlay.

If you aren’t familiar, a Binomial random variable measures the number of successes in a fixed number of Success/Failure trials (denoted by \(n\)). These trials need to be indpendent and have the same probability of success (called \(p\)).

We denote this via \[Y\sim Bin(n, p)\] As \(Y\) measures the number of successes in \(n\) trials, the values \(Y\) can take on are \(y = 0, 1, 2, ..., n\). The probabilities associated with each of these outcomes is given by the Probability Mass Function (PMF) of the Binomial distribution:

\[p_Y(y)= P(Y=y) = \binom{n}{y}p^y(1-p)^{n-y}\]

where \(\binom{n}{y} = \frac{n!}{y!(n-y)!}\) is the binomial coefficient.

We can find these values using the scipy.stats module! Let’s read in the appropriate modules for finding these values and doing our plotting.

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

When writing a function, it is usually easier to write the code for the body of the function outside of a function definition first and then put it into a function.

Let’s start by creating code to find the probabilities associated with the Binomial for a given \(n\) and \(p\). The scipy.stats module has a binom.pmf() function that will return probabilities from the PMF.

print(stats.binom.pmf.__doc__)

Probability mass function at k of the given RV.

        Parameters
        ----------
        k : array_like
            Quantiles.
        arg1, arg2, arg3,... : array_like
            The shape parameter(s) for the distribution (see docstring of the
            instance object for more information)
        loc : array_like, optional
            Location parameter (default=0).

        Returns
        -------
        pmf : array_like
            Probability mass function evaluated at k

Note: the k argument can be ‘array like’. That is, we can pass something like a list of values we want the probabilities for. As a binomial measures the number of successes in \(n\) trials, we need to consider all of the integers from 0 to n. This can be done easily with the range() function.

stats.binom.pmf(0, n = 10, p = 0.5)

0.0009765624999999989

stats.binom.pmf([0,1,2], n = 10, p = 0.5)

array([0.00097656, 0.00976563, 0.04394531])

Ok, we have the values of the random variable (0 to \(n\)) and the probabilities we want to plot. We can use matplotlib’s pyplot module which has a bar() function that can create a basic bar graph for us. It has two arguments:

the x values for the location of the bars
the height for the height of the bars

We just need to pass two things of the same length that correspond to the pairs of x and height.

n = 30
p = 0.5
plt.bar(x = range(n+1), height = stats.binom.pmf(range(n+1), n = n, p = p))

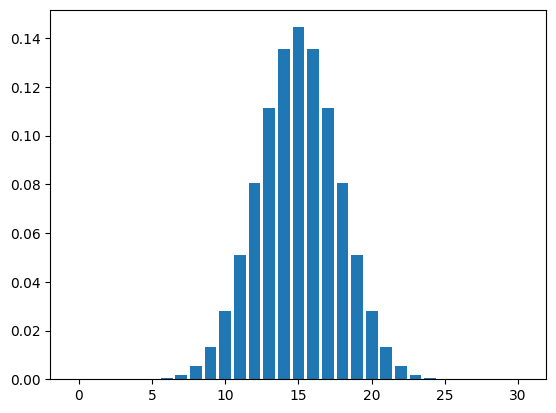
Great! Now let’s wrap that up into a function so the user can call it and just specify n and p. We’ll give default values of n=30 and p=0.5.

def binom_norm_plot(n = 30, p = 0.5):
    plt.bar(x = range(n+1), height = stats.binom.pmf(range(n+1), n = n, p = p))
    return None

binom_norm_plot()

binom_norm_plot(n= 10, p = 0.1)

Now we are cooking! We want to add a curve to this graph corresponding to the commonly used Normal approximation to the binomial.

The Normal distribution has two parameters: mean and standard deviation (or variance)

The mean of the Binomial is \(n*p\) and the standard deviation is \(\sqrt{n*p*(1-p)}\). We can plug these values into the norm.pdf() from the scipy.stats module (PDF stands for Probability Density Function and is the continuous analog to the PMF).

print(stats.norm.pdf.__doc__)

Probability density function at x of the given RV.

        Parameters
        ----------
        x : array_like
            quantiles
        arg1, arg2, arg3,... : array_like
            The shape parameter(s) for the distribution (see docstring of the
            instance object for more information)
        loc : array_like, optional
            location parameter (default=0)
        scale : array_like, optional
            scale parameter (default=1)

        Returns
        -------
        pdf : ndarray
            Probability density function evaluated at x

stats.norm.pdf(0, loc = 0, scale =1)

0.3989422804014327

import math
stats.norm.pdf(range(31), loc = n*p, scale = math.sqrt(n*p*(1-p)))

array([4.45617467e-08, 3.08033680e-07, 1.86349517e-06, 9.86625663e-06,
       4.57162515e-05, 1.85388542e-04, 6.57944456e-04, 2.04357059e-03,
       5.55500081e-03, 1.32151677e-02, 2.75140991e-02, 5.01339573e-02,
       7.99471056e-02, 1.11575174e-01, 1.36278225e-01, 1.45673124e-01,
       1.36278225e-01, 1.11575174e-01, 7.99471056e-02, 5.01339573e-02,
       2.75140991e-02, 1.32151677e-02, 5.55500081e-03, 2.04357059e-03,
       6.57944456e-04, 1.85388542e-04, 4.57162515e-05, 9.86625663e-06,
       1.86349517e-06, 3.08033680e-07, 4.45617467e-08])

Great, now let’s add those values to the plot using the plot() function from pyplot. We’ll learn about this later but if we use matplotlib and create a plot in a cell followed by another plot, it will place those on the same plot by default. Therefore, we just want to create the bar plot and then this other plot in the same cell.

print(plt.plot.__doc__)

Plot y versus x as lines and/or markers.

Call signatures::

    plot([x], y, [fmt], *, data=None, **kwargs)
    plot([x], y, [fmt], [x2], y2, [fmt2], ..., **kwargs)

The coordinates of the points or line nodes are given by *x*, *y*.

The optional parameter *fmt* is a convenient way for defining basic
formatting like color, marker and linestyle. It's a shortcut string
notation described in the *Notes* section below.

>>> plot(x, y)        # plot x and y using default line style and color
>>> plot(x, y, 'bo')  # plot x and y using blue circle markers
>>> plot(y)           # plot y using x as index array 0..N-1
>>> plot(y, 'r+')     # ditto, but with red plusses

You can use `.Line2D` properties as keyword arguments for more
control on the appearance. Line properties and *fmt* can be mixed.
The following two calls yield identical results:

>>> plot(x, y, 'go--', linewidth=2, markersize=12)
>>> plot(x, y, color='green', marker='o', linestyle='dashed',
...      linewidth=2, markersize=12)

When conflicting with *fmt*, keyword arguments take precedence.


**Plotting labelled data**

There's a convenient way for plotting objects with labelled data (i.e.
data that can be accessed by index ``obj['y']``). Instead of giving
the data in *x* and *y*, you can provide the object in the *data*
parameter and just give the labels for *x* and *y*::

>>> plot('xlabel', 'ylabel', data=obj)

All indexable objects are supported. This could e.g. be a `dict`, a
`pandas.DataFrame` or a structured numpy array.


**Plotting multiple sets of data**

There are various ways to plot multiple sets of data.

- The most straight forward way is just to call `plot` multiple times.
  Example:

  >>> plot(x1, y1, 'bo')
  >>> plot(x2, y2, 'go')

- If *x* and/or *y* are 2D arrays a separate data set will be drawn
  for every column. If both *x* and *y* are 2D, they must have the
  same shape. If only one of them is 2D with shape (N, m) the other
  must have length N and will be used for every data set m.

  Example:

  >>> x = [1, 2, 3]
  >>> y = np.array([[1, 2], [3, 4], [5, 6]])
  >>> plot(x, y)

  is equivalent to:

  >>> for col in range(y.shape[1]):
  ...     plot(x, y[:, col])

- The third way is to specify multiple sets of *[x]*, *y*, *[fmt]*
  groups::

  >>> plot(x1, y1, 'g^', x2, y2, 'g-')

  In this case, any additional keyword argument applies to all
  datasets. Also, this syntax cannot be combined with the *data*
  parameter.

By default, each line is assigned a different style specified by a
'style cycle'. The *fmt* and line property parameters are only
necessary if you want explicit deviations from these defaults.
Alternatively, you can also change the style cycle using
:rc:`axes.prop_cycle`.


Parameters
----------
x, y : array-like or scalar
    The horizontal / vertical coordinates of the data points.
    *x* values are optional and default to ``range(len(y))``.

    Commonly, these parameters are 1D arrays.

    They can also be scalars, or two-dimensional (in that case, the
    columns represent separate data sets).

    These arguments cannot be passed as keywords.

fmt : str, optional
    A format string, e.g. 'ro' for red circles. See the *Notes*
    section for a full description of the format strings.

    Format strings are just an abbreviation for quickly setting
    basic line properties. All of these and more can also be
    controlled by keyword arguments.

    This argument cannot be passed as keyword.

data : indexable object, optional
    An object with labelled data. If given, provide the label names to
    plot in *x* and *y*.

    .. note::
        Technically there's a slight ambiguity in calls where the
        second label is a valid *fmt*. ``plot('n', 'o', data=obj)``
        could be ``plt(x, y)`` or ``plt(y, fmt)``. In such cases,
        the former interpretation is chosen, but a warning is issued.
        You may suppress the warning by adding an empty format string
        ``plot('n', 'o', '', data=obj)``.

Returns
-------
list of `.Line2D`
    A list of lines representing the plotted data.

Other Parameters
----------------
scalex, scaley : bool, default: True
    These parameters determine if the view limits are adapted to the
    data limits. The values are passed on to
    `~.axes.Axes.autoscale_view`.

**kwargs : `.Line2D` properties, optional
    *kwargs* are used to specify properties like a line label (for
    auto legends), linewidth, antialiasing, marker face color.
    Example::

    >>> plot([1, 2, 3], [1, 2, 3], 'go-', label='line 1', linewidth=2)
    >>> plot([1, 2, 3], [1, 4, 9], 'rs', label='line 2')

    If you specify multiple lines with one plot call, the kwargs apply
    to all those lines. In case the label object is iterable, each
    element is used as labels for each set of data.

    Here is a list of available `.Line2D` properties:

    Properties:
    agg_filter: a filter function, which takes a (m, n, 3) float array and a dpi value, and returns a (m, n, 3) array and two offsets from the bottom left corner of the image
    alpha: scalar or None
    animated: bool
    antialiased or aa: bool
    clip_box: `.Bbox`
    clip_on: bool
    clip_path: Patch or (Path, Transform) or None
    color or c: color
    dash_capstyle: `.CapStyle` or {'butt', 'projecting', 'round'}
    dash_joinstyle: `.JoinStyle` or {'miter', 'round', 'bevel'}
    dashes: sequence of floats (on/off ink in points) or (None, None)
    data: (2, N) array or two 1D arrays
    drawstyle or ds: {'default', 'steps', 'steps-pre', 'steps-mid', 'steps-post'}, default: 'default'
    figure: `.Figure`
    fillstyle: {'full', 'left', 'right', 'bottom', 'top', 'none'}
    gapcolor: color or None
    gid: str
    in_layout: bool
    label: object
    linestyle or ls: {'-', '--', '-.', ':', '', (offset, on-off-seq), ...}
    linewidth or lw: float
    marker: marker style string, `~.path.Path` or `~.markers.MarkerStyle`
    markeredgecolor or mec: color
    markeredgewidth or mew: float
    markerfacecolor or mfc: color
    markerfacecoloralt or mfcalt: color
    markersize or ms: float
    markevery: None or int or (int, int) or slice or list[int] or float or (float, float) or list[bool]
    mouseover: bool
    path_effects: `.AbstractPathEffect`
    picker: float or callable[[Artist, Event], tuple[bool, dict]]
    pickradius: unknown
    rasterized: bool
    sketch_params: (scale: float, length: float, randomness: float)
    snap: bool or None
    solid_capstyle: `.CapStyle` or {'butt', 'projecting', 'round'}
    solid_joinstyle: `.JoinStyle` or {'miter', 'round', 'bevel'}
    transform: unknown
    url: str
    visible: bool
    xdata: 1D array
    ydata: 1D array
    zorder: float

See Also
--------
scatter : XY scatter plot with markers of varying size and/or color (
    sometimes also called bubble chart).

Notes
-----
**Format Strings**

A format string consists of a part for color, marker and line::

    fmt = '[marker][line][color]'

Each of them is optional. If not provided, the value from the style
cycle is used. Exception: If ``line`` is given, but no ``marker``,
the data will be a line without markers.

Other combinations such as ``[color][marker][line]`` are also
supported, but note that their parsing may be ambiguous.

**Markers**

=============   ===============================
character       description
=============   ===============================
``'.'``         point marker
``','``         pixel marker
``'o'``         circle marker
``'v'``         triangle_down marker
``'^'``         triangle_up marker
``'<'``         triangle_left marker
``'>'``         triangle_right marker
``'1'``         tri_down marker
``'2'``         tri_up marker
``'3'``         tri_left marker
``'4'``         tri_right marker
``'8'``         octagon marker
``'s'``         square marker
``'p'``         pentagon marker
``'P'``         plus (filled) marker
``'*'``         star marker
``'h'``         hexagon1 marker
``'H'``         hexagon2 marker
``'+'``         plus marker
``'x'``         x marker
``'X'``         x (filled) marker
``'D'``         diamond marker
``'d'``         thin_diamond marker
``'|'``         vline marker
``'_'``         hline marker
=============   ===============================

**Line Styles**

=============    ===============================
character        description
=============    ===============================
``'-'``          solid line style
``'--'``         dashed line style
``'-.'``         dash-dot line style
``':'``          dotted line style
=============    ===============================

Example format strings::

    'b'    # blue markers with default shape
    'or'   # red circles
    '-g'   # green solid line
    '--'   # dashed line with default color
    '^k:'  # black triangle_up markers connected by a dotted line

**Colors**

The supported color abbreviations are the single letter codes

=============    ===============================
character        color
=============    ===============================
``'b'``          blue
``'g'``          green
``'r'``          red
``'c'``          cyan
``'m'``          magenta
``'y'``          yellow
``'k'``          black
``'w'``          white
=============    ===============================

and the ``'CN'`` colors that index into the default property cycle.

If the color is the only part of the format string, you can
additionally use any  `matplotlib.colors` spec, e.g. full names
(``'green'``) or hex strings (``'#008000'``).

binom_norm_plot(n = 30, p = 0.5)
n = 30
p = 0.5
plt.plot(range(n+1), stats.norm.pdf(range(n+1), loc = n*p, scale = math.sqrt(n*p*(1-p))))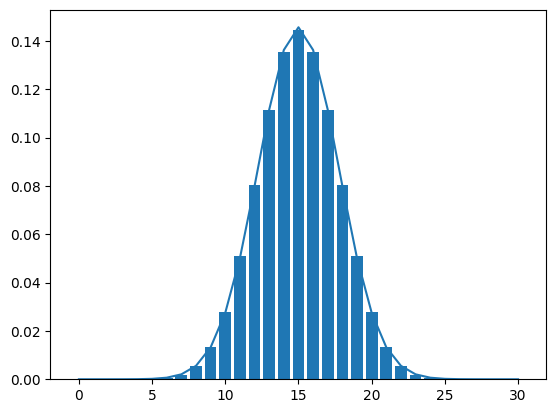

Add that to the function!

def binom_norm_plot(n = 30, p = 0.5):
    plt.bar(x = range(n+1), height = stats.binom.pmf(range(n+1), n = n, p = p))
    plt.plot(range(n+1), stats.norm.pdf(range(n+1), loc = n*p, scale = math.sqrt(n*p*(1-p))))
    return None

binom_norm_plot()

binom_norm_plot(n= 100, p = 0.2)

Control Flow Examples

`for` loop and if/then/else

First, let’s do an if/then/else logic example. Fizz buzz coding!

The logic for the fizz buzz programming problem: - If a number is divisible by 15 (both 3 and 5), then print fizz buzz - If a number is only divisible by 3, then print fizz - If a number is only divisible by 5, then print buzz - Otherwise print the number itself

We can use the % (modulus operator) to get the remainder from a division calculation.

10 % 3

11 % 3

12 % 3

Let’s use if/then/else logic to go through and print the correct statement.

value = 45
if ((value % 5) == 0) and ((value % 3) == 0):
    print("fizz buzz")
elif (value % 3) == 0:
    print("fizz")
elif (value % 5) == 0:
    print("buzz")
else:
    print(value)

fizz buzz

Now wrap it in a for loop to test all numbers between 1 and 100.

for value in range(1, 101):
    if ((value % 5) == 0) and ((value % 3) == 0):
        print("fizz buzz")
    elif (value % 3) == 0:
        print("fizz")
    elif (value % 5) == 0:
        print("buzz")
    else:
        print(value)

1
2
fizz
4
buzz
fizz
7
8
fizz
buzz
11
fizz
13
14
fizz buzz
16
17
fizz
19
buzz
fizz
22
23
fizz
buzz
26
fizz
28
29
fizz buzz
31
32
fizz
34
buzz
fizz
37
38
fizz
buzz
41
fizz
43
44
fizz buzz
46
47
fizz
49
buzz
fizz
52
53
fizz
buzz
56
fizz
58
59
fizz buzz
61
62
fizz
64
buzz
fizz
67
68
fizz
buzz
71
fizz
73
74
fizz buzz
76
77
fizz
79
buzz
fizz
82
83
fizz
buzz
86
fizz
88
89
fizz buzz
91
92
fizz
94
buzz
fizz
97
98
fizz
buzz

`while` loop Example

Let’s do a quick interactive number guessing game. We’ll use the input function to ask the user for an input.

A while loop allows us to keep executing until the user guesses correctly and we update the condition.

input("give me a value ")

give me a value 514kjdaf

'514kjdaf'

truth = 18
correct = False
while not correct:
    guess = int(input("Give me an integer value between 1 and 20: "))
    if guess == truth:
        print("Way to go!")
        correct = True
    elif guess < truth:
        print("Something larger")
    elif guess > truth:
        print("something smaller")

Give me an integer value between 1 and 20: 1
Something larger
Give me an integer value between 1 and 20: 20
something smaller
Give me an integer value between 1 and 20: 19
something smaller
Give me an integer value between 1 and 20: 18
Way to go!

Lists and Tuples Practice

List comprehensions can be confusing at first. Let’s do a little practice. First, let’s write a list comprehension to return a list with values 0, 1, …, 9.

list(range(10))

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

[x for x in range(10)]

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Ok, that is a bit silly but we can do more with this. For instance, we can return \(x^2\) instead of just \(x\).

[x**2 for x in range(10)]

[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

We can also return more than one value if we return a list! Let’s return \(x\), \(x+1\), and \(x+2\).

[[x, x+1, x+2] for x in range(10)]

[[0, 1, 2],
 [1, 2, 3],
 [2, 3, 4],
 [3, 4, 5],
 [4, 5, 6],
 [5, 6, 7],
 [6, 7, 8],
 [7, 8, 9],
 [8, 9, 10],
 [9, 10, 11]]

:Next we’ll consider the map() function, which allows us to apply a function to every element of list (along with other things we’ll look at later!).

Consider applying the sum() function to the first (0th) and second (1st) elements of our list. This should sum the subsequent lists.

y = [[x, x+1, x+2] for x in range(10)]

y[0]

[0, 1, 2]

sum(y[0])

To do this to every list element would be tedious. Instead we can map() the sum() function to each element.

map(sum, y)

<map at 0x7d5be5260b20>

This doesn’t actually return the values! Instead this is an iterator that allows us to find the values when needed.

An easy way to get at these is to just wrap the map in a list().

z = list(map(sum, y))
z

[3, 6, 9, 12, 15, 18, 21, 24, 27, 30]

Next we consider the zip() function, which is quite useful for looking at multiple lists (and other data structures) at once. Here we have two lists of the same length, which we can check with the code below.

print((len(z), len(y)))
zip(z, y)

(10, 10)

<zip at 0x7d5be521bb80>

Now we can write a for loop to iterate over the 0th (first) element of each list at the same time, then the 1st (second) element, …, etc.

for i, j in zip(z, y):
    print(i, j)

3 [0, 1, 2]
6 [1, 2, 3]
9 [2, 3, 4]
12 [3, 4, 5]
15 [4, 5, 6]
18 [5, 6, 7]
21 [6, 7, 8]
24 [7, 8, 9]
27 [8, 9, 10]
30 [9, 10, 11]

This can be done via a list comprehension as well!

[[i,j] for i, j in zip(z,y)]

[[3, [0, 1, 2]],
 [6, [1, 2, 3]],
 [9, [2, 3, 4]],
 [12, [3, 4, 5]],
 [15, [4, 5, 6]],
 [18, [5, 6, 7]],
 [21, [6, 7, 8]],
 [24, [7, 8, 9]],
 [27, [8, 9, 10]],
 [30, [9, 10, 11]]]

[[i,j] for i, j in zip(z,y) if i >12]

[[15, [4, 5, 6]],
 [18, [5, 6, 7]],
 [21, [6, 7, 8]],
 [24, [7, 8, 9]],
 [27, [8, 9, 10]],
 [30, [9, 10, 11]]]

Dictionaries

Let’s construct a dictionary from a tuple and a list. The tuple will act as the keys for our dictionary and the list as the values corresponding to those keys. (We could use lists for both!)

keys = tuple(x for x in "abcdef")
keys

('a', 'b', 'c', 'd', 'e', 'f')

Now we’ll use another list comprehension to return a list where each element is a list itself of length four based on different mathematical functions.

import math
values = [[x, pow(x, 3), math.exp(x), x + 10] for x in range(10, 16)]
values

[[10, 1000, 22026.465794806718, 20],
 [11, 1331, 59874.14171519782, 21],
 [12, 1728, 162754.79141900392, 22],
 [13, 2197, 442413.3920089205, 23],
 [14, 2744, 1202604.2841647768, 24],
 [15, 3375, 3269017.3724721107, 25]]

Using the zip() function on the tuple an dlist, we can easily create a dictionary using the dict() function.

my_dict = dict(zip(keys, values))
my_dict

{'a': [10, 1000, 22026.465794806718, 20],
 'b': [11, 1331, 59874.14171519782, 21],
 'c': [12, 1728, 162754.79141900392, 22],
 'd': [13, 2197, 442413.3920089205, 23],
 'e': [14, 2744, 1202604.2841647768, 24],
 'f': [15, 3375, 3269017.3724721107, 25]}

my_dict["a"]

[10, 1000, 22026.465794806718, 20]

What happens if we convert this dictionary into a list?

list(my_dict)

['a', 'b', 'c', 'd', 'e', 'f']

list(my_dict.values())

[[10, 1000, 22026.465794806718, 20],
 [11, 1331, 59874.14171519782, 21],
 [12, 1728, 162754.79141900392, 22],
 [13, 2197, 442413.3920089205, 23],
 [14, 2744, 1202604.2841647768, 24],
 [15, 3375, 3269017.3724721107, 25]]

list(zip(list(my_dict), list(my_dict.values())))

[('a', [10, 1000, 22026.465794806718, 20]),
 ('b', [11, 1331, 59874.14171519782, 21]),
 ('c', [12, 1728, 162754.79141900392, 22]),
 ('d', [13, 2197, 442413.3920089205, 23]),
 ('e', [14, 2744, 1202604.2841647768, 24]),
 ('f', [15, 3375, 3269017.3724721107, 25])]

We can use any immutable object as our keys. Below we’ll use a tuple as one of our keys and see how to reference that key.

my_dict[(1, "this")] = "this is a string"

my_dict

{'a': [10, 1000, 22026.465794806718, 20],
 'b': [11, 1331, 59874.14171519782, 21],
 'c': [12, 1728, 162754.79141900392, 22],
 'd': [13, 2197, 442413.3920089205, 23],
 'e': [14, 2744, 1202604.2841647768, 24],
 'f': [15, 3375, 3269017.3724721107, 25],
 (1, 'this'): 'this is a string'}

A really useful operator is the in operator. This easily allows us to see if a key exists in a dictionary.

"a" in my_dict

True

"o" in my_dict

False

"o" not in my_dict

True

`NumPy`

We’ll load in the numpy module and create a two-dimensional array using random values from a standard normal distribution.

import numpy as np
rng = np.random.default_rng(10)
values = rng.standard_normal(30)
values

array([-1.10333845, -0.72502464, -0.78180526,  0.26697586, -0.24858073,
        0.12648305,  0.84304257,  0.85793655,  0.47518364, -0.4507686 ,
       -0.75493228, -0.81481411, -0.34385486, -0.05138009, -0.97227368,
       -1.13448753,  0.30570522, -1.85168503, -0.17705351,  0.42582567,
       -0.98535561, -1.11295413, -0.76062603,  0.64802459, -0.12983136,
       -1.86959723, -0.42334911,  1.0138968 ,  0.98371534,  0.63004195])

values.shape

(30,)

values.reshape((15, 2))

array([[-1.10333845, -0.72502464],
       [-0.78180526,  0.26697586],
       [-0.24858073,  0.12648305],
       [ 0.84304257,  0.85793655],
       [ 0.47518364, -0.4507686 ],
       [-0.75493228, -0.81481411],
       [-0.34385486, -0.05138009],
       [-0.97227368, -1.13448753],
       [ 0.30570522, -1.85168503],
       [-0.17705351,  0.42582567],
       [-0.98535561, -1.11295413],
       [-0.76062603,  0.64802459],
       [-0.12983136, -1.86959723],
       [-0.42334911,  1.0138968 ],
       [ 0.98371534,  0.63004195]])

values.reshape((15, 2)).shape

(15, 2)

my_array = values.reshape((15,2))
my_array.base

array([-1.10333845, -0.72502464, -0.78180526,  0.26697586, -0.24858073,
        0.12648305,  0.84304257,  0.85793655,  0.47518364, -0.4507686 ,
       -0.75493228, -0.81481411, -0.34385486, -0.05138009, -0.97227368,
       -1.13448753,  0.30570522, -1.85168503, -0.17705351,  0.42582567,
       -0.98535561, -1.11295413, -0.76062603,  0.64802459, -0.12983136,
       -1.86959723, -0.42334911,  1.0138968 ,  0.98371534,  0.63004195])

We can iterate over values in an array using nditer(). Be careful here: the iteration doesn’t always go through the values in the same pattern as it relies on the memory layout of the array. You can change this behavior though. See https://numpy.org/doc/stable/reference/arrays.nditer.html#arrays-nditer for a discussion and information on how to specify the order.

for i in np.nditer(my_array):
    print(math.exp(i))

0.33176166344167046
0.4843126352266208
0.45757921701143867
1.306008914185862
0.7799068968474736
1.1348302173565885
2.3234254197779323
2.3582894560408887
1.6083095234626505
0.6371382601360868
0.4700424440698853
0.44272161841215146
0.709031831025442
0.9499175441491969
0.3782221046899628
0.3215868817920055
1.3575820587101297
0.15697244006051864
0.8377349576565134
1.5308538739450661
0.37330645316600336
0.32858683744892436
0.4673737442809796
1.911760583275141
0.8782435285725788
0.1541857502671811
0.6548499786487098
2.7563209456441498
2.6743740273453316
1.877689348050752

Many of the functions we’ll apply to arrays are ufuncs or universal functions. These act on an array without requiring the use of explicit looping. They tend to be computationally superior to looping so their use is encouraged! Here we apply the \(e\) function to each element of our array y.

np.exp(my_array)

array([[0.33176166, 0.48431264],
       [0.45757922, 1.30600891],
       [0.7799069 , 1.13483022],
       [2.32342542, 2.35828946],
       [1.60830952, 0.63713826],
       [0.47004244, 0.44272162],
       [0.70903183, 0.94991754],
       [0.3782221 , 0.32158688],
       [1.35758206, 0.15697244],
       [0.83773496, 1.53085387],
       [0.37330645, 0.32858684],
       [0.46737374, 1.91176058],
       [0.87824353, 0.15418575],
       [0.65484998, 2.75632095],
       [2.67437403, 1.87768935]])

If you haven’t seen matrices and the matrix representation of the linear model, you can ignore all of this and just see how we are doing some array computations below.

Let’s fit a simple linear regression model! Suppose we have a 1D response \(y\) and a single predictor (call the vector \(x\)). Then we can find the usual least squares regression line using arrays!

Define \[y = \begin{pmatrix} y_1 \\ y_2 \\ ... \\ y_n\end{pmatrix}\mbox{ our response}\] \[x = \begin{pmatrix} x_1 \\ x_2 \\ ... \\ x_n\end{pmatrix}\mbox{ our predictor}\] We can consider the simple linear regression model: \[y_i = \beta_0+\beta_1 x_i + E_i\] which can be fit by minimizing the sum of squared residuals. Let \(\hat{y}_i = \hat{\beta}_0+\hat{\beta}_1x_i\) denote the prediction for the \(i^{th}\) observation. Then we want to find the \(\hat{\beta}_0\) and \(\hat{\beta}_1\) that minimize \[SS(E) = \sum_{i=1}^{n}(y_i-\hat{y}_i)^2\] This can be minimized by considering the matrix view of the model: Define \[X = \begin{pmatrix} 1 & x_1\\ 1 & x_2 \\ ... \\ 1 & x_n\end{pmatrix}\] and \[\beta = \begin{pmatrix} \beta_0 \\ \beta_1\end{pmatrix}\] Then using matrix multiplication \[X\beta = \begin{pmatrix} \beta_0*1 + \beta_1*x_1\\\beta_0*1 + \beta_1*x_2\\...\\\beta_0*1+\beta_1*x_n\end{pmatrix}\] Our model can be written as

\[y = \begin{pmatrix} y_1 \\ y_2 \\ ... \\ y_n\end{pmatrix} = \begin{pmatrix} \beta_0*1 + \beta_1*x_1\\\beta_0*1 + \beta_1*x_2\\...\\\beta_0*1+\beta_1*x_n\end{pmatrix} + \begin{pmatrix} E_1 \\ E_2 \\ ... \\ E_n\end{pmatrix}\]

or \[y=X\beta + E\]

Then minimizing the \(SS(E)\) can be equivalently written as minimizing over the \(\beta\) vector in \[(y-X\beta)^T(y-X\beta)\] The solution to this equation is \[\hat{\beta} = \begin{pmatrix}\hat{\beta_0} \\\hat{\beta_1} \end{pmatrix} = \left(X^TX\right)^{-1}X^Ty\]

x = np.array([3, 2, 6, 10, 11.2])     #x values
y = -2 + 4*x + rng.standard_normal(5) #create SLR model based response
y

array([ 9.76194119,  4.15506012, 22.16957773, 37.82402224, 42.87679986])

Ok, we want to now fit an SLR model between \(y\) and \(x\) and find estimates of the slope and intercept (true values are -2 and 4).

Let’s create our ‘design matrix’ by zip 1’s (for the intercept) together with our x values.

X = np.array(list(zip(np.ones(5), x)))
X

array([[ 1. ,  3. ],
       [ 1. ,  2. ],
       [ 1. ,  6. ],
       [ 1. , 10. ],
       [ 1. , 11.2]])

We’ll need the transpose of this matrix.

X.transpose()

array([[ 1. ,  1. ,  1. ,  1. ,  1. ],
       [ 3. ,  2. ,  6. , 10. , 11.2]])

And we need to multiply these matrices together.

np.matmul(X.transpose(), X)

array([[  5.  ,  32.2 ],
       [ 32.2 , 274.44]])

Lastly, we need to calculate an matrix inverse. We can do that with the np.linalg.inv() function.

XTXinv = np.linalg.inv(np.matmul(X.transpose(), X))
XTXinv

array([[ 0.81834447, -0.09601622],
       [-0.09601622,  0.01490935]])

Finally, let’s get the least squares solution!

np.matmul(np.matmul(XTXinv, X.transpose()), y)

array([-3.23545354,  4.12933754])

Pretty close to the actual values!

Week 3

Pandas Data Frames

We’ll learn how to read in data using pandas shortly, but here we read in a data file to create a data frame to work with.

There is a dataset on the light measurement quality of cheese at: https://www4.stat.ncsu.edu/~online/datasets/cheese.csv

import pandas as pd
import numpy as np
cheese = pd.read_csv("https://www4.stat.ncsu.edu/~online/datasets/cheese.csv")

We can use the .head() and .info() methods to inspect the data.

cheese.head()

	syrup	rep	L	a	b
0	26	1	51.89	6.22	17.43
1	26	2	51.52	6.18	17.09
2	26	3	52.69	6.09	17.59
3	26	4	52.06	6.36	17.50
4	26	5	51.63	6.13	17.19

cheese.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 24 entries, 0 to 23
Data columns (total 5 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   syrup   24 non-null     int64  
 1   rep     24 non-null     int64  
 2   L       24 non-null     float64
 3   a       24 non-null     float64
 4   b       24 non-null     float64
dtypes: float64(3), int64(2)
memory usage: 1.1 KB

We can also easily add a variable by simply creating a new column reference. Here the value specified is replicated the appropriate amount of times to fill the column. We’ll look at this in more detail later.

cheese["dummy"] = "no"

cheese.head()

	syrup	rep	L	a	b	dummy
0	26	1	51.89	6.22	17.43	no
1	26	2	51.52	6.18	17.09	no
2	26	3	52.69	6.09	17.59	no
3	26	4	52.06	6.36	17.50	no
4	26	5	51.63	6.13	17.19	no

We can reorder the rows of the data frame using the .sort_values() method. Simply specify the column name (or names as a list).

cheese.sort_values("a")

	syrup	rep	L	a	b	dummy
2	26	3	52.69	6.09	17.59	no
5	26	6	52.73	6.12	17.50	no
4	26	5	51.63	6.13	17.19	no
1	26	2	51.52	6.18	17.09	no
0	26	1	51.89	6.22	17.43	no
10	42	5	48.64	6.30	16.21	no
23	62	6	47.88	6.34	15.64	no
3	26	4	52.06	6.36	17.50	no
7	42	2	48.57	6.42	15.91	no
20	62	3	47.35	6.49	15.70	no
22	62	5	46.77	6.66	15.91	no
19	62	2	46.66	6.66	16.30	no
8	42	3	47.57	6.84	16.04	no
18	62	1	45.99	6.84	15.68	no
11	42	6	47.49	6.91	15.91	no
21	62	4	45.83	6.96	15.61	no
9	42	4	46.85	6.97	15.85	no
6	42	1	47.21	7.02	16.00	no
17	55	6	42.65	7.55	14.40	no
16	55	5	42.12	7.56	14.03	no
13	55	2	42.31	7.59	13.98	no
14	55	3	42.31	7.63	14.42	no
15	55	4	41.49	7.66	13.58	no
12	55	1	41.43	7.71	13.74	no

cheese.sort_values(["syrup", "a"])

	syrup	rep	L	a	b	dummy
2	26	3	52.69	6.09	17.59	no
5	26	6	52.73	6.12	17.50	no
4	26	5	51.63	6.13	17.19	no
1	26	2	51.52	6.18	17.09	no
0	26	1	51.89	6.22	17.43	no
3	26	4	52.06	6.36	17.50	no
10	42	5	48.64	6.30	16.21	no
7	42	2	48.57	6.42	15.91	no
8	42	3	47.57	6.84	16.04	no
11	42	6	47.49	6.91	15.91	no
9	42	4	46.85	6.97	15.85	no
6	42	1	47.21	7.02	16.00	no
17	55	6	42.65	7.55	14.40	no
16	55	5	42.12	7.56	14.03	no
13	55	2	42.31	7.59	13.98	no
14	55	3	42.31	7.63	14.42	no
15	55	4	41.49	7.66	13.58	no
12	55	1	41.43	7.71	13.74	no
23	62	6	47.88	6.34	15.64	no
20	62	3	47.35	6.49	15.70	no
19	62	2	46.66	6.66	16.30	no
22	62	5	46.77	6.66	15.91	no
18	62	1	45.99	6.84	15.68	no
21	62	4	45.83	6.96	15.61	no

We can add some NaN or not a number values. These represent missing data values. For a discussion of why this isn’t None, see https://stackoverflow.com/questions/17534106/what-is-the-difference-between-nan-and-none

cheese.loc[0:3, "dummy"] = np.nan
cheese.head()

	syrup	rep	L	a	b	dummy
0	26	1	51.89	6.22	17.43	NaN
1	26	2	51.52	6.18	17.09	NaN
2	26	3	52.69	6.09	17.59	NaN
3	26	4	52.06	6.36	17.50	NaN
4	26	5	51.63	6.13	17.19	no

We can then drop any rows that contain a NaN value (in any column) with .dropna(). This doesn’t overwrite the object.

cheese.dropna()

	syrup	rep	L	a	b	dummy
4	26	5	51.63	6.13	17.19	no
5	26	6	52.73	6.12	17.50	no
6	42	1	47.21	7.02	16.00	no
7	42	2	48.57	6.42	15.91	no
8	42	3	47.57	6.84	16.04	no
9	42	4	46.85	6.97	15.85	no
10	42	5	48.64	6.30	16.21	no
11	42	6	47.49	6.91	15.91	no
12	55	1	41.43	7.71	13.74	no
13	55	2	42.31	7.59	13.98	no
14	55	3	42.31	7.63	14.42	no
15	55	4	41.49	7.66	13.58	no
16	55	5	42.12	7.56	14.03	no
17	55	6	42.65	7.55	14.40	no
18	62	1	45.99	6.84	15.68	no
19	62	2	46.66	6.66	16.30	no
20	62	3	47.35	6.49	15.70	no
21	62	4	45.83	6.96	15.61	no
22	62	5	46.77	6.66	15.91	no
23	62	6	47.88	6.34	15.64	no

cheese.head()

	syrup	rep	L	a	b	dummy
0	26	1	51.89	6.22	17.43	NaN
1	26	2	51.52	6.18	17.09	NaN
2	26	3	52.69	6.09	17.59	NaN
3	26	4	52.06	6.36	17.50	NaN
4	26	5	51.63	6.13	17.19	no

We can also fill in any NaN values using .fillna(). This also doesn’t overwrite the object.

cheese.fillna("yes")

	syrup	rep	L	a	b	dummy
0	26	1	51.89	6.22	17.43	yes
1	26	2	51.52	6.18	17.09	yes
2	26	3	52.69	6.09	17.59	yes
3	26	4	52.06	6.36	17.50	yes
4	26	5	51.63	6.13	17.19	no
5	26	6	52.73	6.12	17.50	no
6	42	1	47.21	7.02	16.00	no
7	42	2	48.57	6.42	15.91	no
8	42	3	47.57	6.84	16.04	no
9	42	4	46.85	6.97	15.85	no
10	42	5	48.64	6.30	16.21	no
11	42	6	47.49	6.91	15.91	no
12	55	1	41.43	7.71	13.74	no
13	55	2	42.31	7.59	13.98	no
14	55	3	42.31	7.63	14.42	no
15	55	4	41.49	7.66	13.58	no
16	55	5	42.12	7.56	14.03	no
17	55	6	42.65	7.55	14.40	no
18	62	1	45.99	6.84	15.68	no
19	62	2	46.66	6.66	16.30	no
20	62	3	47.35	6.49	15.70	no
21	62	4	45.83	6.96	15.61	no
22	62	5	46.77	6.66	15.91	no
23	62	6	47.88	6.34	15.64	no

We can get a lot of summary statistics easily from a data frame using the .describe() method.

cheese.describe()

	syrup	rep	L	a	b
count	24.000000	24.000000	24.000000	24.000000	24.000000
mean	46.250000	3.500000	47.151667	6.800417	15.800417
std	14.013193	1.744557	3.691321	0.559895	1.239907
min	26.000000	1.000000	41.430000	6.090000	13.580000
25%	38.000000	2.000000	45.035000	6.330000	15.312500
50%	48.500000	3.500000	47.280000	6.750000	15.910000
75%	56.750000	5.000000	49.360000	7.152500	16.497500
max	62.000000	6.000000	52.730000	7.710000	17.590000

Reading Raw Data with Pandas

Below we’ll check our working directory and then read in a SAS file using read_sas() from pandas.

import os
os.getcwd()

'/content'

pd.read_sas("air.sas7bdat")

	DATE	AIR
0	1949-01-01	112.0
1	1949-02-01	118.0
2	1949-03-01	132.0
3	1949-04-01	129.0
4	1949-05-01	121.0
...	...	...
139	1960-08-01	606.0
140	1960-09-01	508.0
141	1960-10-01	461.0
142	1960-11-01	390.0
143	1960-12-01	432.0

144 rows × 2 columns

Numerical Summaries

Contingency Tables

We’ll import pandas and read in a data set about NFL games. The data has information about games from 2002 to 2014. Each row represents one game and each column a variable measured on that game.

Available here: https://www4.stat.ncsu.edu/~online/datasets/scoresFull.csv

import pandas as pd
scores = pd.read_csv("https://www4.stat.ncsu.edu/~online/datasets/scoresFull.csv")
scores.head()

	week	date	day	season	awayTeam	AQ1	AQ2	AQ3	AQ4	AOT	...	homeFumLost	homeNumPen	homePenYds	home3rdConv	home3rdAtt	home4thConv	home4thAtt	homeTOP	HminusAScore	homeSpread
0	1	5-Sep	Thu	2002	San Francisco 49ers	3	0	7	6	-1	...	0	10	80	4	8	0	1	32.47	-3	-4.0
1	1	8-Sep	Sun	2002	Minnesota Vikings	3	17	0	3	-1	...	1	4	33	2	6	0	0	28.48	4	4.5
2	1	8-Sep	Sun	2002	New Orleans Saints	6	7	7	0	6	...	0	8	85	1	6	0	1	31.48	-6	6.0
3	1	8-Sep	Sun	2002	New York Jets	0	17	3	11	6	...	1	10	82	4	8	2	2	39.13	-6	-3.0
4	1	8-Sep	Sun	2002	Arizona Cardinals	10	3	3	7	-1	...	0	7	56	6	10	1	2	34.40	8	6.0

5 rows × 82 columns

We can use the pd.cut() function to take a numeric variable and chop it up into groups. Note: generally splitting a numeric variable into categories isn’t a great idea. You lose information!

pd.cut(scores.AtotalYds, bins = [0, 150, 250, 400, 700])

0       (250, 400]
1       (250, 400]
2       (250, 400]
3       (250, 400]
4       (250, 400]
           ...    
3466    (250, 400]
3467    (250, 400]
3468    (250, 400]
3469    (150, 250]
3470    (250, 400]
Name: AtotalYds, Length: 3471, dtype: category
Categories (4, interval[int64, right]): [(0, 150] < (150, 250] < (250, 400] < (400, 700]]

Great, but we can improve the categories being produced for the category variable. We just need to specify the labels argument and have the same number of labels as the number of categories produced.

scores["AtotalYdsCut"] = pd.cut(scores.AtotalYds, bins = [0, 150, 250, 400, 700], labels = ["Poor", "Ok", "Good", "Great"])

Now we can easily create a one-way table to display the number of occurrences of each category using the .value_counts() method.

scores.AtotalYdsCut.value_counts()

Good     2082
Great     706
Ok        611
Poor       72
Name: AtotalYdsCut, dtype: int64

Let’s create a similar variable for the away team total yards and create a two-table using the pd.crosstab() function.

scores["HtotalYdsCut"] = pd.cut(scores.HtotalYds, bins = [0, 150, 250, 400, 700], labels = ["Poor", "Ok", "Good", "Great"])
pd.crosstab(scores.HtotalYdsCut, scores.AtotalYdsCut)

AtotalYdsCut	Poor	Ok	Good	Great
HtotalYdsCut
Poor	0	5	20	10
Ok	4	56	282	101
Good	43	399	1354	396
Great	25	151	426	199

Numeric Variable Summaries with `pd.pivot_table()`

In addition to the methods/functions used in the notes, we can also create summary stats across groups using the pivot_table() function and the .agg() method.

First let’s look at the pivot_table() function. We need to supply a data frame, the columns we want to summarize (as values), the grouping variable(s) (as index), and the aggregation function(s) (as aggfunc).

pd.pivot_table(scores, values = "AtotalYds", index = "season")

	AtotalYds
season
2002	324.161049
2003	308.247191
2004	321.161049
2005	308.378277
2006	316.449438
2007	321.906367
2008	318.760300
2009	323.977528
2010	329.734082
2011	341.655431
2012	347.089888
2013	340.685393
2014	343.310861

We can give more than one function if we specify it as a list.

pd.pivot_table(scores, values = "AtotalYds", index = "season", aggfunc = ["mean", "median", "std"])

	mean	median	std
	AtotalYds	AtotalYds	AtotalYds
season
2002	324.161049	327	90.314948
2003	308.247191	311	88.807591
2004	321.161049	318	90.912791
2005	308.378277	304	82.750663
2006	316.449438	323	79.343217
2007	321.906367	327	82.208671
2008	318.760300	317	86.567603
2009	323.977528	323	86.360668
2010	329.734082	327	88.964809
2011	341.655431	336	86.608624
2012	347.089888	352	88.788882
2013	340.685393	341	83.003251
2014	343.310861	343	83.797760

We can also group by more than one variable by specify the variables as a list.

pd.pivot_table(scores, values = "AtotalYds", index = ["season", "week"], aggfunc = ["mean", "median", "std"])

		mean	median	std
		AtotalYds	AtotalYds	AtotalYds
season	week
2002	1	310.000000	286.0	70.386552
	10	352.857143	367.0	76.175766
	11	299.125000	332.5	98.892450
	12	357.750000	348.0	97.722396
	13	314.062500	302.0	104.683949
...	...	...	...	...
2014	9	344.769231	364.0	96.695531
	ConfChamp	257.500000	257.5	68.589358
	Division	367.250000	363.0	46.399533
	SuperBowl	396.000000	396.0	NaN
	WildCard	257.000000	276.5	133.434129

273 rows × 3 columns

`.agg()` method

The .agg() method gives us another way to create summary stats. We can create a variable and pass a tuple containing the column to summarize and the function to use when summarizing.

scores.agg(max_AtotalYds = ("AtotalYds", "max"))

	AtotalYds
max_AtotalYds	622

We can create multiple summaries easily by specifying more than one variable. These summaries also respect the groupby() groupings!

scores.groupby("season").agg(max_AtotalYds = ("AtotalYds", "max"))

	max_AtotalYds
season
2002	591
2003	548
2004	605
2005	494
2006	536
2007	531
2008	564
2009	524
2010	592
2011	622
2012	583
2013	542
2014	596

scores \
.groupby("season") \
.agg(max_AtotalYds = ("AtotalYds", "max"),
     min_AtotalYds = ("AtotalYds", "min"))

	max_AtotalYds	min_AtotalYds
season
2002	591	47
2003	548	96
2004	605	26
2005	494	113
2006	536	104
2007	531	104
2008	564	125
2009	524	72
2010	592	67
2011	622	137
2012	583	119
2013	542	103
2014	596	78

Week 4

More Function Writing

Let’s look at the use of a lambda function as the key to the sorted() function. We’ll use a toy data set we create with an id column that we want to sort by.

We can use list comprehensions to generate ids of the form ‘id#’ and some cost values we just make up. Then we’ll put those into a data frame to inspect.

import pandas as pd
nums = [4, 10, 22, 5, 12, 1]
ids = ["id" + str(x) for x in nums]
cost = [21, 32, 12, 0, 23, 43]
print(ids, cost)

['id4', 'id10', 'id22', 'id5', 'id12', 'id1'] [21, 32, 12, 0, 23, 43]

Put those into a data frame.

my_df = pd.DataFrame(cost, index = ids, columns = ["cost"])
my_df

	cost
id4	21
id10	32
id22	12
id5	0
id12	23
id1	43

Now let’s see how the sorted function acts on the ids column.

sorted(my_df.index)

['id1', 'id10', 'id12', 'id22', 'id4', 'id5']

Not quite what we want! We can sort with a key. A lambda function can be used to make a quick function that will take the id column’s value and look at the 2nd element on, converting that to an int.

Passing this as the function to use for the key will give us what we want!

sorted(my_df.index, key = lambda x: int(x[2:]))

['id1', 'id4', 'id5', 'id10', 'id12', 'id22']

Now we can sort the data frame using this sorting.

my_df.loc[sorted(my_df.index, key = lambda x: int(x[2:]))]

	cost
id1	43
id4	21
id5	0
id10	32
id12	23
id22	12

Investigating the LLN

Let’s use our find_means() function to see the behavior of the sample mean when the sample size gets large samples.

In this case, we are generating data from a standard normal distribution. This is the population distribution. Since we are generating the data ourselves, we know that the actual mean of the population here is 0. In statistics we often try to estimate these population quantities. Our usual estimator of the population mean is the sample mean. Ideally our estimator should be observed really close to the truth (population value) when our sample size grows!

A statistical theory called the Law of Large Numbers (LLN) says that the behavior of sample average type statistics should get closer to the population value as the sample size grows.

We can demonstrate this behavior by using our find_means() function for increasingly large random samples from the standard normal distribution! We know the true value is 0 so we can see how close it gets using our simulations.

First, let’s create our find_means() function and bring in numpy as needed.

import numpy as np
from numpy.random import default_rng
rng = default_rng(3)

def find_means(*args, decimals = 4):
    """
    Assume that args will be a bunch of numpy arrays (1D) or pandas series
    """
    means = []
    for x in args: #iterate over the tuple values
        means.append(np.mean(x).round(decimals))
    return means

Now we can use map() to create samples of varying sizes easily!

standard_normal_data = map(rng.standard_normal, range(1, 51))

Now we can pass that list using * to unpack it. The elements will be read into the unlimited positional argument we defined, args.

find_means(*standard_normal_data)

[2.0409,
 -1.0688,
 -0.412,
 0.0515,
 -0.4263,
 0.1058,
 0.5156,
 0.2256,
 -0.5504,
 0.3226,
 -0.5999,
 0.0015,
 -0.0263,
 -0.0402,
 0.1694,
 0.3517,
 -0.0175,
 -0.0879,
 0.5763,
 -0.0086,
 -0.3138,
 0.0313,
 0.3178,
 0.1171,
 -0.2855,
 0.0906,
 0.0179,
 0.1475,
 0.3238,
 -0.0359,
 0.091,
 0.241,
 0.1158,
 0.0413,
 0.0656,
 -0.0811,
 0.2771,
 -0.1547,
 -0.1708,
 -0.151,
 -0.0666,
 0.0119,
 0.0339,
 0.1983,
 -0.1047,
 -0.0413,
 0.1733,
 0.0081,
 0.1325,
 -0.0272]

Plotting matplotlib

Let’s take our function that was able to output many means from normal random samples and use it to make a plot! This will visualize the result we were seeing.

Let’s first manually create the plot, then put the plot functionality into a function! We really have a sample size associated with each of these means. Let’s first create a data frame that has the sample size and the calculated mean.

standard_normal_data = map(rng.standard_normal, range(1, 51))
my_means = find_means(*standard_normal_data)
mean_df = pd.DataFrame(zip(my_means, range(1,51)), columns = ["means", "n"])
mean_df.head()

	means	n
0	-1.4405	1
1	0.2436	2
2	0.1613	3
3	-0.4510	4
4	-0.3320	5

Now import matplotlib.pyplot and let’s make a plot!

import matplotlib.pyplot as plt
plt.scatter(mean_df.n, mean_df.means)
plt.axhline(y = 0, color = 'r', linestyle = '-')

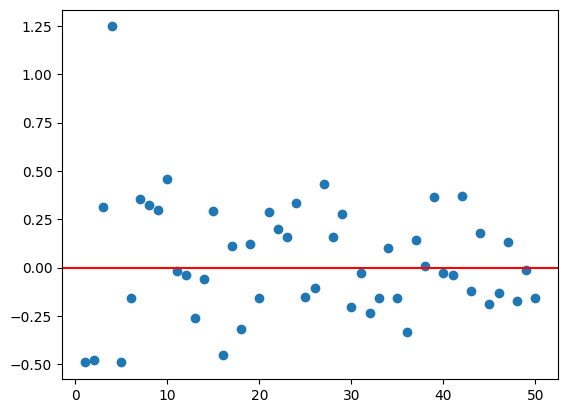
Great, now let’s make a function that does this for us! The function will just take in a sample size and then produce the plot from that. Our find_means() function will be used as a helper function.

def plot_means(n = 50):
  standard_normal_data = map(rng.standard_normal, range(1, n+1))
  my_means = find_means(*standard_normal_data)
  mean_df = pd.DataFrame(zip(my_means, range(1, n+1)), columns = ["means", "n"])
  plt.scatter(mean_df.n, mean_df.means)
  plt.axhline(y = 0, color = 'r', linestyle = '-')

plot_means(10)

plot_means(1000)

Plotting with pandas

Let’s revisit our NFL data example from previous. We’ll then look at line plots.

import pandas as pd
scores = pd.read_csv("https://www4.stat.ncsu.edu/~online/datasets/scoresFull.csv")
scores.head()

	week	date	day	season	awayTeam	AQ1	AQ2	AQ3	AQ4	AOT	...	homeFumLost	homeNumPen	homePenYds	home3rdConv	home3rdAtt	home4thConv	home4thAtt	homeTOP	HminusAScore	homeSpread
0	1	5-Sep	Thu	2002	San Francisco 49ers	3	0	7	6	-1	...	0	10	80	4	8	0	1	32.47	-3	-4.0
1	1	8-Sep	Sun	2002	Minnesota Vikings	3	17	0	3	-1	...	1	4	33	2	6	0	0	28.48	4	4.5
2	1	8-Sep	Sun	2002	New Orleans Saints	6	7	7	0	6	...	0	8	85	1	6	0	1	31.48	-6	6.0
3	1	8-Sep	Sun	2002	New York Jets	0	17	3	11	6	...	1	10	82	4	8	2	2	39.13	-6	-3.0
4	1	8-Sep	Sun	2002	Arizona Cardinals	10	3	3	7	-1	...	0	7	56	6	10	1	2	34.40	8	6.0

5 rows × 82 columns

We saw we could get summaries of the data in a number of ways. One was the .agg() method.

scores \
.groupby("season") \
.agg(max_AtotalYds = ("AtotalYds", "max"),
     min_AtotalYds = ("AtotalYds", "min"))

	max_AtotalYds	min_AtotalYds
season
2002	591	47
2003	548	96
2004	605	26
2005	494	113
2006	536	104
2007	531	104
2008	564	125
2009	524	72
2010	592	67
2011	622	137
2012	583	119
2013	542	103
2014	596	78

Line graphs are especially useful when you have data over time. For instance, the summary above is over season. We can put season on the x-axis and see how our summaries change over time. The plot.line() method is great for creating these types of plots. It prefers data where each column will be plotted and the index represents the time. That is exactly what we have outputted from above!

Let’s add a mean and median variable for the AtotalYds and then create a line plot for these four variables.

summaries = scores \
.groupby("season") \
.agg(max_AtotalYds = ("AtotalYds", "max"),
     min_AtotalYds = ("AtotalYds", "min"),
     mean_AtotalYds = ("AtotalYds", "mean"),
     median_AtotalYds = ("AtotalYds", "median"))
summaries.head()

	max_AtotalYds	min_AtotalYds	mean_AtotalYds	median_AtotalYds
season
2002	591	47	324.161049	327.0
2003	548	96	308.247191	311.0
2004	605	26	321.161049	318.0
2005	494	113	308.378277	304.0
2006	536	104	316.449438	323.0

summaries.plot()

Error Handling

Let’s use our find_means() function and add a try block to keep processing if one of our arguments passed isn’t appropriate.

def find_means(*args, decimals = 4):
    """
    Assume that args will be a bunch of numpy arrays (1D) or pandas series
    """
    means = []
    for x in args: #iterate over the tuple values
        means.append(np.mean(x).round(decimals))
    return means

find_means(np.array([1,2,3,6, "hi"]))

---------------------------------------------------------------------------
UFuncTypeError                            Traceback (most recent call last)
<ipython-input-83-a4c06acf4d92> in <cell line: 1>()
----> 1 find_means(np.array([1,2,3,6, "hi"]))

<ipython-input-82-06de86f374b0> in find_means(decimals, *args)
      5     means = []
      6     for x in args: #iterate over the tuple values
----> 7         means.append(np.mean(x).round(decimals))
      8     return means

/usr/local/lib/python3.10/dist-packages/numpy/core/overrides.py in mean(*args, **kwargs)

/usr/local/lib/python3.10/dist-packages/numpy/core/fromnumeric.py in mean(a, axis, dtype, out, keepdims, where)
   3430             return mean(axis=axis, dtype=dtype, out=out, **kwargs)
   3431 
-> 3432     return _methods._mean(a, axis=axis, dtype=dtype,
   3433                           out=out, **kwargs)
   3434 

/usr/local/lib/python3.10/dist-packages/numpy/core/_methods.py in _mean(a, axis, dtype, out, keepdims, where)
    178             is_float16_result = True
    179 
--> 180     ret = umr_sum(arr, axis, dtype, out, keepdims, where=where)
    181     if isinstance(ret, mu.ndarray):
    182         ret = um.true_divide(

UFuncTypeError: ufunc 'add' did not contain a loop with signature matching types (dtype('<U21'), dtype('<U21')) -> None

def find_means(*args, decimals = 4):
    """
    Assume that args will be a bunch of numpy arrays (1D) or pandas series
    """
    means = []
    for x in args: #iterate over the tuple values
        try:
            means.append(np.mean(x).round(decimals))
        except TypeError:
            print("It appears that the data type is wrong!")
            means.append(np.nan)
    return means

find_means(np.array([1,2,3,6, "hi"]))

It appears that the data type is wrong!

[nan]

find_means(np.array([424,13,13]), np.array([1,2,3,6, "hi"]), np.array(["yo"]))

It appears that the data type is wrong!
It appears that the data type is wrong!

[150.0, nan, nan]

Week 1

Basics of python

Markdown

Strings Practice

Math Types (Including Booleans)

Week 2

User Defined Functions

Control Flow Examples

for loop and if/then/else

while loop Example

Lists and Tuples Practice

Dictionaries

NumPy

Week 3

Pandas Data Frames

Reading Raw Data with Pandas

Numerical Summaries

Contingency Tables

Numeric Variable Summaries with pd.pivot_table()

.agg() method

Week 4

More Function Writing

Investigating the LLN

Plotting matplotlib

Plotting with pandas

Error Handling

`for` loop and if/then/else

`while` loop Example

`NumPy`

Numeric Variable Summaries with `pd.pivot_table()`

`.agg()` method